Die Leistungsübertragungsfähigkeit von Transformatoren

An einem Freitagnachmittag wollte ich gerade vom Büro nach Hause gehen, als das Telefon klingelte. Ein Kunde hat eine interessante Frage gestellt. Dies stammt von einem 30-VA-50-Hz-Transformator, den wir für ihn entworfen hatten, der aber tatsächlich in einer 40-VA-Anwendung verwendet wird. „Welche Auswirkungen hätte diese Betriebssituation also auf den Transformator?“, fragte der Ingenieur des Kunden am anderen Ende der Leitung.

Wenn man das Design des Transformators kennt, kann seine Nennleistung definitiv auf 40 VA erhöht werden, wobei die größten Auswirkungen offensichtlich ein zusätzlicher Temperaturanstieg von etwa 10 °C und ein leichter Abfall der Ausgangsspannung bei Volllast sind. Der Grund ist natürlich, dass die Ausgangslast erhöht wird. Der Ingenieur fuhr fort: „Wenn wir den Temperaturanstieg nicht berücksichtigen, ist es dann richtig anzunehmen, dass die Leistung dieses Transformators unendlich gesteigert werden kann?“ Als ich seiner Vermutung zuhörte, dass die Leistungsübertragung des Transformators möglicherweise unendlich erhöht wird, sagte ich: „Das ist unmöglich, die Leistung des Transformators wird überlaufen (ein sogenannter „Leistungsüberlauf“), wie der Kaffee in einer Kaffeetasse überlaufen wird, da die Tasse eine begrenzte Volumenkapazität hat.“

Bei diesem Problem geht es in der Tat um die Leistungsübertragungsfähigkeit des Transformators. Um diese Frage zu beantworten, ist ein Transformator-Ersatzschaltbild ein guter Ausgangspunkt. Theoretisch ist der ideale Leistungstransformator ein Gerät, das weder Energie produziert, speichert noch verbraucht. Es überträgt lediglich die Leistung vom Stromnetz zum Verbraucher, indem es die Primär- und Sekundärspannung gemäß dem festgelegten Windungsverhältnis ändert. In Wirklichkeit wird die Leistung des Transformators jedoch aufgrund der Eigenverluste von Eisenkernen (Kernverlust) und des Vorhandenseins von Wicklungswiderständen (Kupferverlust) nicht zu 100 % übertragen. Die Eingangs- und Ausgangsspannung des Transformators ist also keine einfache Beziehung des Windungsverhältnisses. Dies lässt sich aus dem Zweitor-Ersatzschaltbild des in Abb. 1 unten gezeigten Transformators erklären.

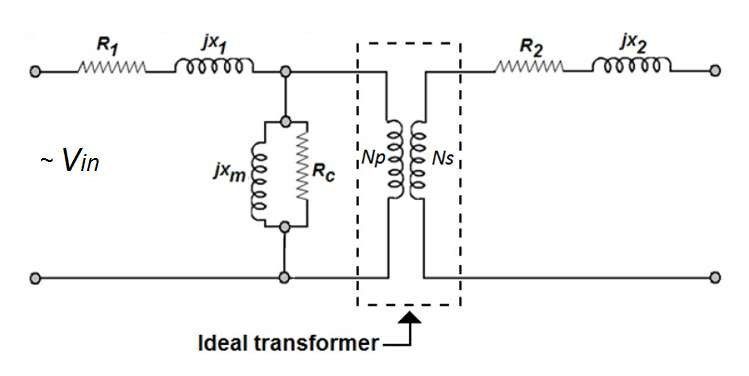
Dabei ist Vin die Eingangsversorgungsspannung, R1 der Primärwicklungswiderstand des Transformators, X1 die Primärstreureaktanz des Transformators, Rc der äquivalente Kernverlustwiderstand des Transformators und Xm die Erregerreaktanz des Transformators. R2 ist der Sekundärwicklungswiderstand des Transformators und X2 ist die Sekundärstreureaktanz des Transformators.

Solange die Primärwicklung an eine Spannungsquelle angeschlossen ist, induziert die Sekundärwicklung des Transformators eine Ausgangsspannung. Im Leerlauf des Transformators entsteht auch bei offenem Sekundärkreis eine Schleife im Primärkreis, die zu einem Stromfluss durch den Primärkreis führt. Dieser Strom wird „Leerlaufstrom“ genannt. Im Allgemeinen ist der äquivalente Kernwiderstand Rc viel größer als die Transformatorreaktanz Xm (d. h. Rc >> Xm), sodass der Leerlaufstrom des Transformators als Erregerstrom des Transformators betrachtet werden kann. Es ist dieser Erregerstrom, der das Arbeitsmagnetfeld des Transformators (mit Flussdichte B bezeichnet) aufbaut und seine Funktion zur Änderung der Ausgangsspannung erfüllt.

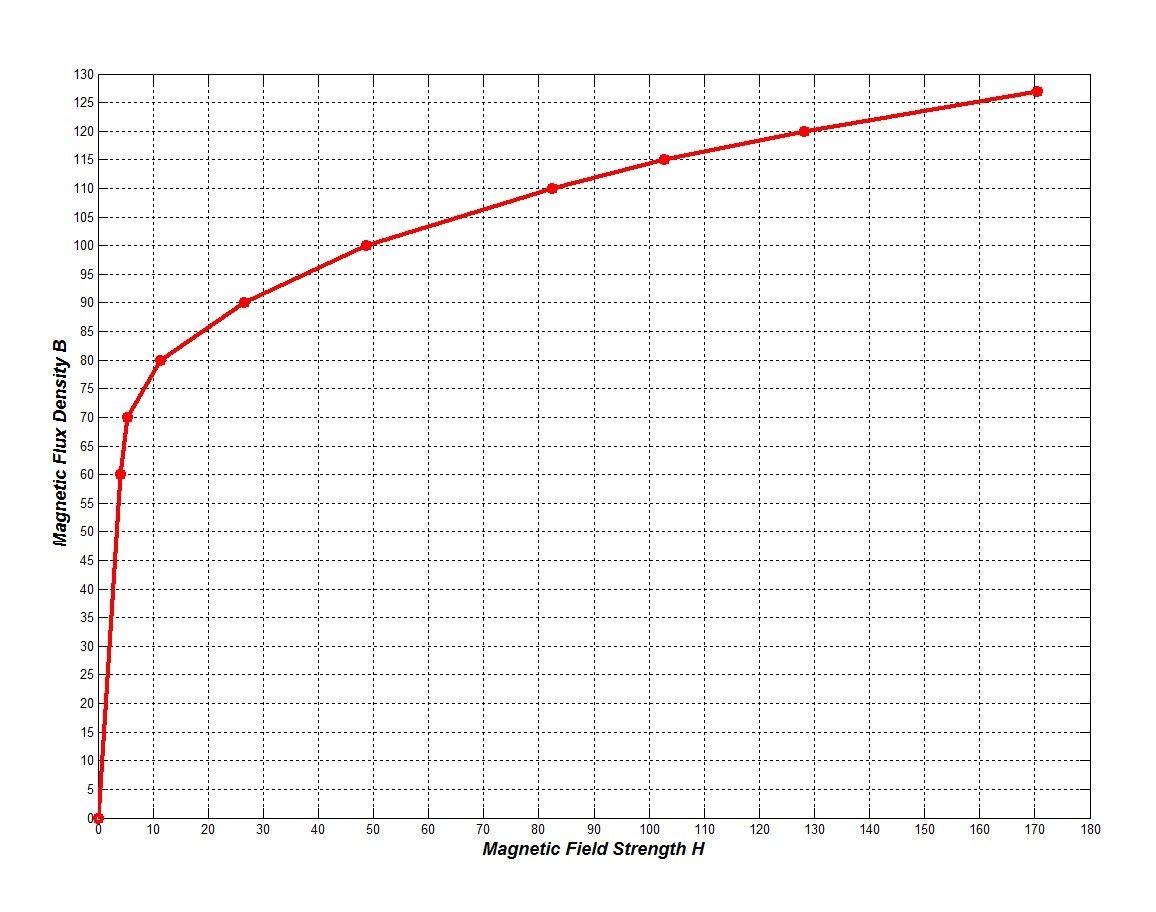
(Diese Kurve ist aus praktischen Ergebnissen abgeleitet und weicht geringfügig vom theoretischen Ergebnis ab.)

Diese B-H-Kurve kann in drei Abschnitte unterteilt werden. Der erste Abschnitt davon ist die Magnetverlustkompensationsstufe, gefolgt von dem Abschnitt mit schnellem Flussanstieg in der Mitte und schließlich dem Magnetfluss-Sättigungsbereich, d. h. dem nach rechts gebogenen Teil der B-H-Kurve. Wenn der Erregerstrom des Transformators sehr klein ist, erzeugt er die an den Kern angelegte magnetische Feldstärke H; der Kern wird dann magnetisiert und das entsprechend erzeugte Magnetfeld ist nicht stark. In diesem Stadium ändert sich die B-H-Kurve sanft. Wenn der Feldstrom ansteigt, wird der Kern magnetisiert, um einen schnellen Anstieg des Magnetflusses zu erzeugen. Daher ist die B-H-Kurve in diesem Stadium sehr steil. Wenn der Erregerstrom des Transformators auf ein bestimmtes Niveau ansteigt, ist die Änderung der magnetischen Feldstärke ∆H viel größer als die Änderung der magnetischen Flussdichte ∆B. Dadurch erreicht der Trafokern die Sättigung. In diesem Stadium wird die B-H-Kurve flach.

Wenn wir als Konstrukteur von Transformatoren einen Transformator innerhalb der vom Kunden angegebenen Nennleistung entwerfen, wollen wir auf keinen Fall einen großen und sperrigen Transformator entwerfen, der die Leistungsanforderungen erfüllt. Wir betrachten die Kompromisse, um ein optimales Gleichgewicht zwischen Leistung, Größe und Herstellbarkeit sowie anderen Faktoren zu erhalten. Daher sollte jeder Transformator so nah wie möglich an seiner maximalen Leistungsübertragungsfähigkeit ausgelegt werden, mit einem angemessenen Temperaturanstieg. Um die Verwendung von Kernmaterialien zu maximieren, ist es wichtig, die magnetische Arbeitsinduktionsdichte B so nahe wie möglich am Ende der zweiten Stufe der B-H-Kurve zu wählen, wo die Kurve beginnt, sich horizontal zu drehen.

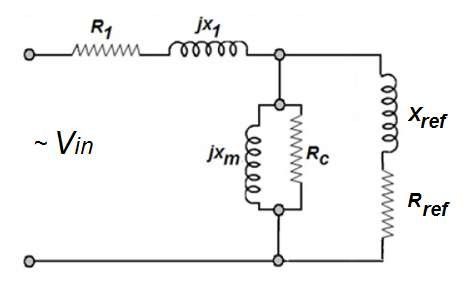
Abbildung 3 zeigt das Ersatzschaltbild eines Transformators im belasteten Zustand, wobei der Sekundärkreis im belasteten Zustand zum Primärkreis reflektiert wird. Im Allgemeinen ist die Eingangsspannung für einen 50-Hz-Abwärtstransformator die Netzspannung, die von 100 V bis 240 V variiert, sodass die Anzahl der Windungen in der Primärwicklung groß ist. Daher ist der Wert der Anregungsreaktanz Xm viel größer, verglichen mit der sekundär reflektierten Impedanz zur Primärseite. Wenn sich die Eingangsspannung nicht ändert, bleibt der Erregerstrom unverändert, wenn man den Spannungsabfall vernachlässigt, der durch die Impedanz der Primärwicklung verursacht wird. Gleichzeitig erhöht sich auch der Strom der Primärseite, da er genügend Energie an die Last übertragen wird. Mit anderen Worten, der erhöhte Strom im Primärstrom wird verwendet, um den durch die Sekundärlast erzeugten Strom auszugleichen. Es wurde bereits gesagt, dass ein idealer Transformator ein Gerät ist, das Energie weder produziert, speichert noch verbraucht.

Der Transformator kann als Strom-/Energieübertragungsleitung betrachtet werden. Wenn die Last unendlich erhöht wird (wie vom Ingenieur des Kunden vorgeschlagen), steigt der Strom auf der Primärseite mit zunehmendem Sekundärstrom. Der Spannungsabfall an der Primärwicklung erhöht sich entsprechend. Es ist erwähnenswert, dass die tatsächlich in den Felderregerkreis geladene Spannung verringert wird und der tatsächliche Magnetisierungsstrom des Transformators niedriger wird; und die sekundär induzierte Spannung wird ebenfalls kleiner. Gleichzeitig wird der Spannungsabfall der Sekundärwicklung größer, was zu einer deutlichen Reduzierung der Lastspannung führt. Diese Änderungen sind in Abb. 4 deutlich zu sehen.

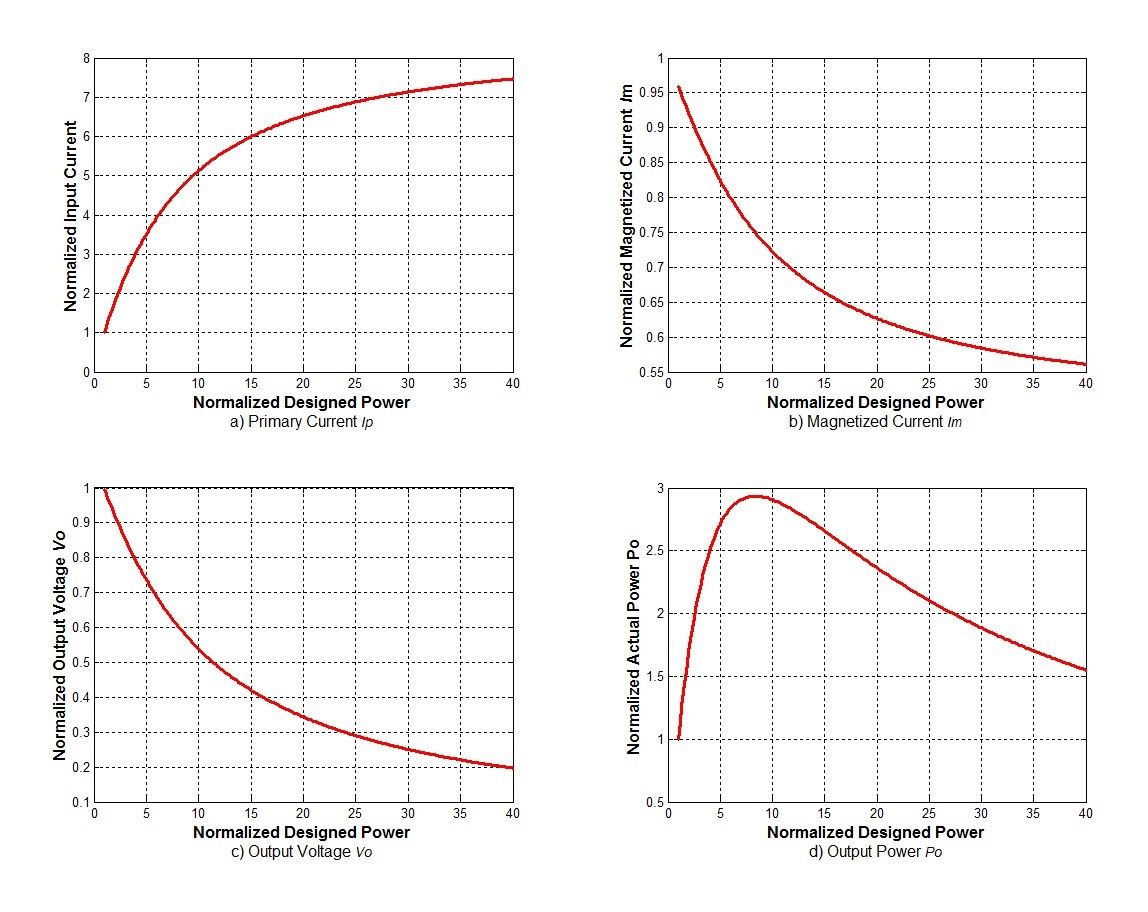
Es wird davon ausgegangen, dass ein Transformator eine viermal höhere Leistung als die ursprüngliche Nennleistung abgeben soll, d.h. der Ausgangsblindwiderstand beträgt 1/5 des Nennlastwertes. Aus Abb. 4 a) geht hervor, dass der Eingangsstrom des Transformators jetzt um das 2,5-fache des Nennstroms erhöht wird, während in Abb. 4b) der Erregerstrom nur noch 87 % des ursprünglichen Erregerstroms beträgt; Gleichzeitig wird die tatsächliche Ausgangsspannung des Transformators auf 75 % der ursprünglichen Nennspannung reduziert, wie in 4c) gezeigt. Die tatsächliche Ausgangsleistung soll aber auf das 5-fache der Nennleistung gesteigert werden, tatsächlich erreicht sie nur das 2,7-fache der Nennleistung. Dies ist in Abb. 4d) deutlich zu sehen, wo es einen maximalen Punkt in der Leistungsübertragungskurve gibt. Wenn die gewünschte Leistung das 7-fache der Nennleistung übersteigt, erreicht der Transformator die maximale Leistungsübertragungskapazität. Die tatsächlich maximal übertragene Leistung beträgt jedoch nur etwa das 3-fache der Nennleistung. Dies nennen wir den zuvor in diesem Artikel erwähnten „Leistungsüberlauf“. Das bedeutet, dass sobald die Kerngröße des Transformators bestimmt ist, auch seine maximale Leistungsübertragungsfähigkeit bestimmt und vorhersagbar ist.

Es ist wichtig darauf hinzuweisen, dass nicht der Strom, sondern die Eingangsspannung den Sättigungsgrad eines Transformatorkerns dominiert. In der Entwurfsphase des Transformators ist es wichtig, die maximale magnetische Flussdichte B aus der B-H-Kurve der Kerneigenschaften, die von den Lieferanten bereitgestellt werden, richtig auszuwählen. Beachten Sie, dass die Eingangsspannung des Transformators den Kernverlust des Transformators bestimmt und der Transformatorstrom den Kupferverlust des Transformators dominiert.

Wenn der Kernverlust des Transformators konstant ist, bedeutet eine Erhöhung des Transformatorstroms gleichzeitig eine Erhöhung des Kupferverlusts des Transformators. Dies beschleunigt den Anstieg des Transformatortemperaturanstiegs. Aufgrund des Vorhandenseins von Kupferverlusten wird die unbegrenzte Erhöhung der Übertragungsleistung des Transformators eingeschränkt.

Im Allgemeinen lautet die Faustregel für die Konstruktion eines 50-Hz-Transformators, die geeignete magnetische Flussdichte B sorgfältig auszuwählen, um sicherzustellen, dass der Transformator nicht gesättigt wird. Wählen Sie zweitens die richtige Wicklungsdrahtstärke, damit der Temperaturanstieg des Transformators in einem angemessenen Bereich für die Transformatoranwendung liegt und der Energieverbrauch optimiert wird. Da nachhaltige Entwicklung heute die neue Norm ist, erfordert dies, dass ein Konstrukteur diese Regeln bei der Entwurfsplanung berücksichtigt.